Suppose you have some theory R, formulated in that fragment of English that is free of semantic vocabulary. The theory, we can assume, is at least “effectively” classical—e.g. we can assume excluded middle and so forth for each predicate that it uses. Now think of total theory—which includes not just this theory but also, e.g. a theory of truth.
It would be nice if truth in this widest theory could work “transparently”—so that we could treat “p” and “T(p)” as intersubstitutable at least in all extensional contexts. To get that, something has to go. E.g. the logic for the wider language might have to be non-classical, to avoid the Liar paradox.
One question is whether weakening logic is enough to avoid problems. For all we’ve said so far, it might be that one can have a transparent truth-predicate—but only if one’s non-semantic theories are set up just right. In the case at hand, the worry is that R cannot be consistently embedded within a total theory that includes a transparent truth predicate. Maybe in order to ensure consistency of total theory, we’d have to play around with what we say in the non-semantic fragment. It’d be really interesting if we could get a guarantee that we never need to do that. And this is one thing that Kripke’s fixed point construction seems to give us.
Think of Kripke’s techniques as a “black box”, which takes as input classical models of the semantics-free portion of our language, and outputs non-classical models of language as a whole—and in such a way as to make “p” and “Tp” always coincide in semantic value. Crucially, the non-classical model coincides with the classical model taken as input when it comes to the semantics-free fragment. So if “S” is in the semantics-free language and is true-on-input-model, then it will be true-on-the-output model.
This result seems clearly relevant to the question of whether we disrupt theories like R by embedding them within a total theory incorporating transparent truth. The most obvious thought is to let M be the intended (classical) model of our base language—and then view the Kripke construction as outputting a candidate to be the intended interpretation of total language. And the result just given tells us that if R is true relative to M, it remains true relative to the outputted Kripkean (non-classical model).
But this is a contentious characterization. For example, if our semantics-free language contains absolutely unrestricted quantifiers, there won’t be a (traditional) model that can serve as the “intended interpretation”. For (traditional) models assign sets as the range of quantifiers, and no set contains absolutely everything—in particular no set can contain all sets. And even if somehow we could finesse this (e.g. if we could argue that our quantifiers can never be absolutely unrestricted), it’s not clear that we should be identifying true-on-the-output-model with truth, which is crucial to the above suggested moral.
Field suggests we take a different moral from the Kripkean construction. Focus on the question of whether theories like R (which ex hypothesi are consistent taken alone), might turn out to be inconsistent in the light of total theory—in particular, might turn out to be inconsistent once we’ve got a transparent truth predicate in our language. He argues that the Kripkean construction gives us this.
Here’s the argument. Suppose that R is classically consistent. We want to know whether R+T is consistent, where R+T is what you get from R when you add in a transparent truth-predicate. The consistency of R means that there’s a classical model on which it is true. Input that into Kripke’s black box. And what we get out the other end is a (non-classical) model of R+T. And the existence of such a model (whether or not it’s an “intended one”) means that R+T is consistent.
Field explicitly mentions one worry about this–that it might equivocate over “consistent”. If consistent just means “has a model (of such-and-such a kind)” then the argument goes through as it stands. But in the present setting it’s not obvious what all this talk of models is doing for us. After all, we’re not supposed to be assuming that one among the models is the “intended” one. In fact, we’re supposed to be up for the thesis that the very notion of “intended interpretation” should be ditched, in which case there’d be no space even for viewing the various models as possibly, though not actually, intended interpretations.
This is the very point at which Kreisel’s squeezing argument is supposed to help us. For it forges a link between intuitive consistency, and the model-theoretic constructions. So we could reconstruct the above line of thought in the following steps:
- R is consistent (in the intuitive sense)
- So: R is consistent (in the model-theoretic sense). [By a squeezing argument]
- So: R+T is consistent (in the model-theoretic sense). [By the Kripkean construction]
- So: R+T is consistent (in the intuitive sense). [By the squeezing argument again]
Now, I’m prepared to think that the squeezing argument works to bridge the gap between (1) and (2). For here we’re working within the classical fragment of English, and I see the appeal of the premises of the squeezing argument in that setting (actually, for this move we don’t really need the premise I’m most concerned with—just the completeness result and intuitive soundness suffice).
But the move from (3) to (4) is the one that I find dodgy. For this directly requires the principle that if there is a formal (3-valued) countermodel to a given argument, then that argument is invalid (in the intuitive sense). And that is exactly the point over which I voiced scepticism in the previous post. Why should the recognition that there’s an assignment of values to R+T on which an inference isn’t value-1 preserving suggest that the argument from R+T to absurdity is invalid? Without illegitimately sneaking in some thoughts about what value-1 represents (e.g. truth, or determinate truth) I can’t even begin to get a handle on this question.
In the previous post I sketched a fallback option (and it really was only a sketch). I suggested that you might run a squeezing argument for Kleene logic using probabilistic semantics, rather than 3-valued ones, since we do have a sense of what a probabilistic assignment represents, and why failure to preserve probability might be an indicator of intuitive invalidity. Now maybe if this were successful, we could bridge the gap—but in a very indirect way. One would argue from the existence of a 3-valued model, via completeness, to the non-existence of a derivation of absurdity from R+T. And then, by a second completeness result, one would argue that there had to exist a probabilistic model for R+T. Finally, one would appeal to the general thought that such probabilistic models secured consistency (in the intuitive sense).
To summarize. The Kripkean constructions obviously secure a technical conservativeness result. As Field mentions, we should be careful to distinguish this from a true conservativeness result: the result that no inconsistency can arise from adding transparent truth to a classically consistent base theory. But whether the technical result we can prove gives us reason (via a Kreisel-like argument) to believe the true conservativeness result turns on exactly the issue of whether a 3-valued countermodel to an argument gives us reason to think that that argument is intuitively invalid. And it’s not obvious at all where that last part is coming from—so for me, for now, it remains open whether the Kripkean constructions give us reason to believe true conservativeness.

That’s an interesting idea to use the probabilistic semantics for the squeezing argument. Is the jist supposed to be that: if an ideally rational agent could believe it, then it must be consistent?
I guess I didn’t really get the motivating worry though. Suppose R is a complete set of sentences characterising English minus semantic vocabulary. Then truth-in-a-model of R just *is* truth, since we have assumed R is complete. (Whether or not the quantifiers are interpreted as unrestricted.)
Even if R is incomplete (suppose e.g. it’s plural ZFCU), I’m told most set theorists believe in some kind of global reflection principle – which means for some , truth-in-
, truth-in- *just is* truth. So even if we can’t get the *intended* model to characterise truth, there’s a substitute that’s close enough.
*just is* truth. So even if we can’t get the *intended* model to characterise truth, there’s a substitute that’s close enough.
Or is the worry that if you put anything other than the intended model into the black-box, it might output something other than truth? I didn’t think that could happen if you took the minimal one – but maybe someone who knows more than me could confirm that.
It would be interesting to see if you could extend the Kripke constructions to the Rayo/Uzquiano/Williamson model theory done in a second order metalanguage. I can’t see any reason why you couldn’t, but I don’t really know enough about that stuff.
Hi Andrew, thanks for the comments!
On the motivating thought. I don’t think I assumed R was complete—but rather, just that there was a completeness theorem for the logic. R might be e.g. “grass is green” + “London is in the UK”. Both are true—but can we get a general reassurance that such R won’t be disrupted when we add transparent truth to the mix?
I’m interested in the global reflection principle you mention. Could you point me to where it’s formulated and discussed? (I’m just trying to think through what happens to Tarki’s theorem for the theory ZFC+that reflection principle+the relevant T-sentences—I guess that folks in the literature will have sorted this out already!).
Here’s one general thought: set theoretic reflection principles aren’t obviously going to help if the ground language we’re interested in contains non-set-theoretic vocabulary—and so if the R we’re interested in contains not just the axioms of ZFCU but also a bunch of empirical truths…. there might still be a set where truth on a model taking that set as domain coincides with truth simpliciter, but the question is a bit different, I think, from the purely set theoretic case. (Especially if e.g. we think that there are more urrelemente than sets).
I do agree it’s interesting to think through this stuff in connection with the stuff that Rayo et al are doing. Here’s one thing that seems important to me about the way that Field is conceiving of Kripkean constructions: it’s important for him that the metalanguage in which we carry through the construction can be viewed as a fragment of the object-language under consideration. If you wanted to preserve the availability of that standpoint, then if you used second order quantifiers in the metalanguage, you’d have to build the construction around an object-language that was also second order.
Of course, not every way of interpreting the Kripkean constructions will motivate the constraint just mentioned. But from the point of view of someone aiming to defend semantically closed languages, it’s particularly natural.
Hey Robbie,
I wouldn’t worry about Tarski’s theorem – the global reflection principle on its own doesn’t allow you to *define* a truth predicate (to get a description referring to our proxy intended model, you’d have to say stuff like “take the epsilon-minimal set that models all the true sentences of set theory.” But of course, we can only say that if the truths are recursive – we’ve basically just proven they can’t be.)
To be honest I really don’t know where to go to find out what set theorists think about it. Rayo and Uzquiano state discuss it and have some remarks pertinent to you question on Tarski’s theorem here:
Click to access puzzle.pdf
I think Peter Koellner writes on them, that’s probably the best place to go. To see how they relate to squeezing arguments, Shapiro has a piece ‘Principles of Reflection and Second Order Logic’ in JPL. (Although squeezing arguments won’t work for SOL, since it lacks a completeness theorem, it turns out the reflection principle I mentioned is equivalent to the second order analogue of Kreisels conclusion.)
Anyway, I hadn’t really thought what would happen if there were more urelements than sets. Most people I talk to are quite hostile to this possibility, but it seems quite plausible to me, especially if you have unrestricted composition, even for sets, or you think every single set has a heicceity (or you take things like Kaplans paradox seriously.) I think Williamson and Rayo’s completeness proof for their logic for unrestricted languages relies on there being as many sets as urelements, so I guess it’s looking less hopeful that reflection principles would help us there.
BTW I was talking to Field the other week about Rayo & co, and he pretty much had the same reaction. Note, though, that you *can* give a second order model theory for languages with second order quantification – it’s just that the metalanguage must contain a second level predicate ‘Sat(M, x, v)’ which the object language can’t.
Thanks Andrew—I’ll have to look this up. BTW, do you envisage appealing to the reflection principle in the metalanguage to make the argument go through? That would seem to do the work you wanted it to, though it’d raise again the question of the relation between meta-language and object-language.
Or do you think it can be unproblematically expressed in the object-language?
The Shapiro reference seems promising—but I can’t get e-access to it right now so I’ll have to try to get hold of it some other way.
Ah I now see your question. Yes, the principle I was envisaging is stated in the metalanguage.
As to your second question, I reckon you *could* state it in the object language. Note that the reflection principle just says that there’s some set such that any formula in the language of ZFC that’s true, is true with its quantifiers restricted to that set. It doesn’t say anything about formulae in the language of ZFC + “true”. So if we just add a truth predicate, and axiomatise it a la Tarski’s theory of satisfaction then we can say:
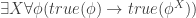
 is like phi except with all quantifiers restricted to X. (My quantifying over formulae is implicitly over sentences in ZFC language – not ZFC+truth language.)
is like phi except with all quantifiers restricted to X. (My quantifying over formulae is implicitly over sentences in ZFC language – not ZFC+truth language.)
where
Coincidentally, we got talking about whether the Kripke stuff would work out in cases where the intended model was a proper class in one of my seminars today. It sounded like it wouldn’t – but as far as I could see, the only reason was because things stopped being set sized.
Actually, coming to think of it, I think the Shapiro paper has an object language statement of the reflection principle. It’s been ages since I read it though.
Hey Robbie,
I was just re-reading ch.3 or the Field where this stuff gets discussed. I noticed something, which I think relates to this post.
So Field gives up on identifying truth with having semantic value 1, and so will give up on identifying validity with preservation of semantic value 1 in any model. So what’s the point of the Kripke construction? It’s supposed to do two things: give us the conservativeness result you mention and show us how to tell what inferences are legitimate in KFS. But one of its drawbacks is that it doesn’t let us say things about the liar sentence that we’d like to say, e.g. that it’s defective.
At this point, Field introduces the idea that the advocate of KFS might try to communicate their take on the liar by saying that they neither accept it nor reject it. That is then cashed out in terms of degrees of belief. We’ve got to drop classical ideas, and in particular, we give up on the idea that P(A) + P(not-A) should sum to 1. Field also reckons that the KFS theorist will need to invoke the notions of conditional acceptance and conditional rejection.
He then writes:
“These notions [conditional acceptance/rejection] will have an important role to play in KFS. For instance, one of the reasons for the importance of the notion of logical consequence is that if B is a logical consequence of A then we should conditionally accept B on the assumption of A; and [the definition of conditional acceptance Field offers] provides for this. Indeed, the advocate of KFS is to explain logical consequence of than in model-theoretic terms, I think it would have to be in terms of laws of conditional belief. It certainly can’t be as necessary truth-preservation.” p. 75
That struck me as an having an obvious relation to the probabilistic justification of the squeezing arguments you mentioned in the post.
Thoughts?
Hi Rich;
Field does deny Truth=Semantic value 1. But he doesn’t deny that validity (at least extensionally coincides with) semantic value 1 preservation. Indeed, what he denies is that validity is truth preservation. The squeezing argument would be an argument for the extensional coincidence.
The passage you quote is interesting—of course, it’s a bit unclear what “explaining consequence” amounts to. But given that in the past he used (classical) conditional probabilities to formally characterize classical consequence, then it’s a natural thought that we might try to generalize that to this setting. What I’d like to know is the formal details…
Ah, right – the only thought was that it looked, at least to me, like Field was intimating that the conditional probabilities stuff could be used to forge a link between intuitive-validity and KFSmodel-theoretic validity.
Where is the stuff you allude to where Field uses classical conditional probabilities to characterize classical consequence?
It’s in his 1977 JP piece, “Logic, meaning and conceptual role”.